2.3 平面作画

作画というとき、一般には計算は用いないが、造船現図ではそう限定しないでよい。より能率が上るのなら計算も役立てる。

先に示したように直角三角形の場合、ピタゴラスの定理が使える。

[実長]2＝[スペース]2＋[落ち]2

この式からスペースごとに物指を作り〔落ち〕を測れば〔伸び〕が読取れるようにすると便利である（図2.2.7）。この関数尺を実長尺と呼ぶ。

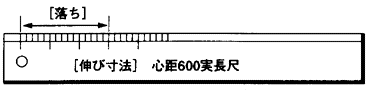
図2.2.7

さて、実長には、その線の含まれる平面を取出せばよかった。実名も同様で、その角の含まれる面を出せばよい。先の実長を求めた直角三角形で、線とその影のなす角度は、実長と同時に求められている。

ここで一般の三角形の性格を再確認しておこう（図2.2.8）。

・三角形は、一平面を決める。

・三角形は、三辺の長さで決まる。

・三角形は、二辺とそのなす角で決まる。

・三角形は、一辺とその両端角で決まる。理屈としては、一辺とどの二角ででも決まるのであるが、三つの角の合計は2直角であり、作画上は両端角とする。

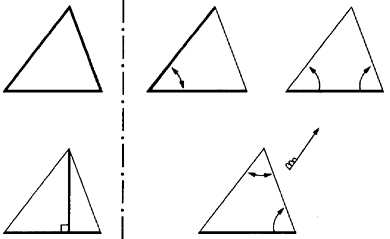
図2.2.8

一般に現図作画には、角度は用いない方がよい。分度器では足が短いため精度が劣り、自在金は狂いが出易い。使うならコンパスで正確に出せる直角だけとしたい。

・三角形は、一辺とその対応頂点からの垂線で決まる。この最後の直角三角形の構成にする方法は現図展開で多用されている。角度には三種ある。

・線と線の交角：

これまでの説明で見た角度

・線と面の交角：

線を含み、面に直交する面を想定すれば、その想定面に表わされる角度（図2.2.9）

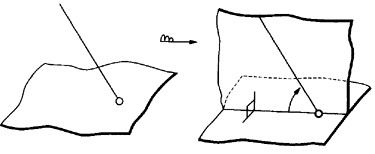
図2.2.9

前ページ　　　目次へ　　　次ページ